Science : Term 1 Unit 1 : Measurement
Evaluation
I. Choose the appropriate answer:
1. Which of the following is a derived unit?
a. mass
b. time
c. area
d. length
Answer: c) area
2. Which of the following is correct?
a. 1L= 1cc
b. 1L= 10 cc
c. 1L= 100 cc
d. 1L= 1000 cc
Answer: d) 1L = 1000 cc
3. SI unit of density is
a. kg/m2
b. kg/m3
c. kg/m
d. g/m3
Answer: b) kg/m3
4. Two spheres have equal mass and volume in the ratio 2:1. The ratio of their density is
a. 1:2
b. 2:1
c. 4:1
d. 1:4
Answer: a) 1:2
5. Light year is the unit of
a. Distance
b. time
c. density
d. both length and time
Answer: a) Distance
II. Fill in the blanks
1.Volume of irregularly shaped objects are measured using the law of displacement.
2. One cubic metre is equal to 106 cubic centimetre.
3. Density of mercury is 13,600 kg m-3.
4. One astronomical unit is equal to 1.496 × 1011m.
5. The area of a leaf can be measured using a graph sheet.
III. State whether the following statements are true or false:
1. The region covered by the boundary of the plane figure is called its volume. [False]
The region covered by the boundary of the plane figure is called its area.
2. Volume of liquids can be found using measuring containers. [True]
3. Water is denser than kerosene. [True]
4. A ball of iron floats in mercury. [True]
5. A substance which contains less number of molecules per unit volume is said to be denser. [False]
A substance which contains more number of molecules per unit volume is said to be denser.
IV. Match the items in column-I to the items in column-II:
(1)
Column-I – Column-II
i. Area (a) light year
ii. Distance (b) m3
iii. Density (c) m2
iv. Volume (d) kg
v. Mass (e) kg / m3
Answer:
Column-I Column-II
i. Area : (c) m2
ii. Distance : (a) light year
iii. Density : (e) kg / m3
iv. Volume : (b) m3
v. Mass : (d) kg
(2)
Column-I – Column-II
i. Area (a) g / cm3
ii. Length (b) measuring jar
iii. Density (c) amount of a substance
iv. Volume (d) rope
v. Mass (e) plane figures
Answer :
Column-I : Column-II
i. Area : (e) plane figures
ii. Length : (b) rope
iii. Density : (a) g/cm3
iv. Volume : (b) measuring jar
v. Mass (c) amount of a substance
V. Arrange the following in correct sequence:
1. 1L, 100 cc, 10 L, 10 cc
Answer: 10 cc, 100 cc, 1 L, 10L
2. Copper, Aluminium, Gold, Iron
Answer: Aluminium, Iron, Copper, Gold.
VI. Use the analogy to fill in the blank:
1. Area: m2 :: Volume: m3
2. Liquid: Litre :: Solid: cm3
3. Water: kerosene :: Iron : Aluminium
VII. Assertion and reason type questions:
Mark the correct choice as
a. If both assertion and reason are true and reason is the correct explanation of assertion.
b. If both assertion and reason are true, but reason is not the correct explanation of assertion.
c. Assertion is true but reason is false.
d. Assertion is false but reason is true.
1. Assertion: Volume of a stone is found using a measuring cylinder.
Reason: Stone is an irregularly shaped object.
2. Assertion: Wood floats in water.
Reason: Water is a transparent liquid.
3. Assertion: Iron ball sinks in water.
Reason: water is denser than iron.
Answer :
1) a. If both assertion and reason are true and reason is the correct explanation of assertion.
2) b. If both assertion and reason are true, but reason is not the correct explanation of assertion.
3) c. Assertion is true but reason is false.
VIII. Give very short answer:
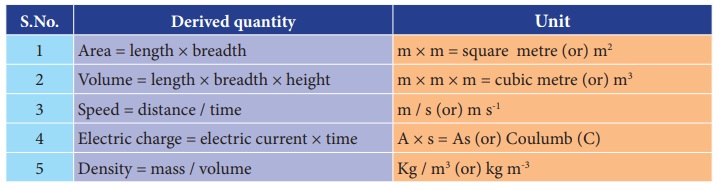
1. Name some of the derived quantities.
Area, volume, speed, electric charge, density
2. Give the value of one light year.
9.46 × 1015 m
3. Write down the formula used to find the volume of a cylinder.
πr2h
r – radius
h – height
4. Give the formula to find the density of objects.
(D) = Mass (M) / Volume (V)
5. Name the liquid in which an iron ball sinks.
water
6. Name the units used to measure the distance between celestial objects.
i) Astronomical Unit
ii) Light year
7. What is the density of gold?
19,300 kgm-3
IX. Give short answer:
1. What are derived quantities?
2. Distinguish between the volume of liquid and capacity of a container.
The volume of any liquid is equal to the space that it fills and it can be measured using a measuring cylinder or measuring beaker.
The maximum volume of liquid that a container can hold is known as the “capacity of the container”.
3. Define the density of objects.
Density of a substance is defined as the mass of the substance contained in unit volume ( 1 m3).
If the mass of a substance is “M” whose volume is “V”, then, the equation for density is given as
Density (D) = mass (M) / volume (V)
D = M / V
4. What is one light year?
One light year is defined as the distance travelled by light in vacuum during the period of one year.
1 Light year = 9.46 × 10l5 m.
5. Define -one astronomical unit?
One astronomical unit is defined as the average distance between the earth and the sun.
1 AU = 149.6 million km = 1.496 × 1011 m.
X. Answer in detail.
1. Describe the graphical method to find the area of an irregularly shaped plane figure.
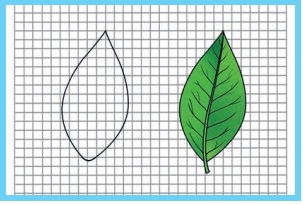
We can find the area irregular figures with the help of a graph sheet. Place the leaf on a graph sheet and draw the outline of the leaf with a pencil You can see the outline of the leaf on the graph sheet.
i) Now, count the number of whole squares enclosed within the outline of the leaf. Take it to be M.
ii) Then, count the number of squares that are more than half. Take it as N.
iii) Next, count the number of squares which are half of a whole square. Note it lo be P.
iv) Finally, count the number of squares that are less than half. Let it be Q.
Now, the approximate area of the leaf can be calculated using the following formula:
Approximate area of the leaf = M + (¾)N + (½)P + (¼)Q square cm. This formula can be used to calculate the area of any irregulary shaped plane figures.
2. How will you determine the density of a stone using a measuring jar?
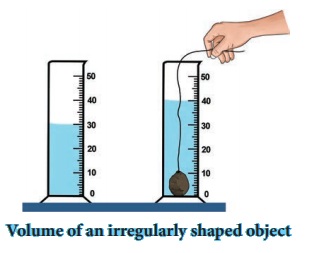
Take a measuring cylinder and pour some water into it (Do not fill the cylinder completely). Note down the volume of water from the readings of the measuring cylinder. Take it as V1. Now take a small stone and tie it with a thread. Immerse the stone inside the water by holding the thread. This has to be done such that the stone does not touch the walls of the measuring cylinder (Figure).
Now, the level of water has raised. Note down the volume of water and take it to beV2.
The volume of the stone is equal to the raise in the volume of water.
V1, = 30CC ; V2 = 40 CC;
Volume of stone = V2 – V1,
= 40 – 30 = 10 CC.
Measure the mass of the stone = M = 50 g (say)
Then density = Mass / Volume = 50 / 10cc = 5g/cc
density = 5 g / cm3
XI. Questions based on Higher Order Thinking skills:
1. There are three spheres A, B, C as shown below:
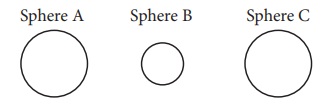
Sphere A and B are made of the same material. Sphere C is made of a different material. Spheres A and C have equal radii. The radius of sphere B is half that of A. Density of A is double that of C. Now answer the following questions:
i. Find the ratio of masses of spheres A and B.
ii. Find the ratio of volumes of spheres A and B.
iii. Find the ratio of masses of spheres A and C.
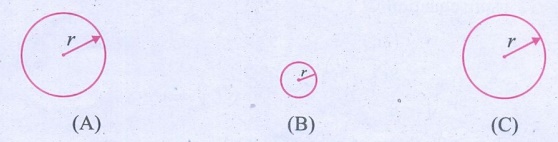
From the given particulars
rm = 2r6 ……………….(1)
ra = rc …………… ( 2)
da = db ………(3)
da = 2dc ……….(4)
From equation (2)
Va = Vc ………………….(5)
Here r – radius; d – density; V-volume
i) Find the ratio of masses of spheres A and B.
mass = density × volume
Mass of A : Mass of B
(volume of A × density of A) : (volume of B × density of B)
4/3 π r3a × da : 4/3 π r3b × db
Using equations (1), and (3)
(2rb)3 × db : r3b db
8r3b : r 3b
8 : 1
Ratio of mass of spheres A & B = 8:1
ii) Find the ratio of volumes of spheres A and B.
Volume of a sphere 4/3 π r3a
Volume of A : Volume of B
4/3 π r3a : 4/3 π r3b
Using equation (1)
(2rb)3 : r3b
8r3b : r3b
8 : 1
Ratio of volume of spheres = 8:1
iii) Find the ratio of masses of spheres A and C.
Mass = Volume × density
Mass of A = Mass of C
Va × da = Vc × dc
using equations (4),( 5),
Vc × 2dc : Vc × dc
2 : 1
∴ Ratio of mass of spheres A & C is 2 : 1
XII. Numerical problems:
1. A circular disc has a radius 10 cm. Find the area of the disc in m2. (Use π = 3.14).
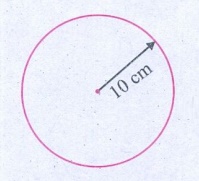
Radius = 10cm
100 cm = 1 m
∴ 10 cm = 10 / 100 m = 0.1m
∴ Radius of the circle = 10-1 m
Area of the circle = πr2
= 3.14 × (10-1 m × 10-1 m
= 3.14 × l0-2 m2
2. The dimension of a school playground is 800 m × 500 m. Find the area of the ground.
It is a Rectangular Shaped Ground
Its area = ? × b
= 800 m × 500 m
= 8 × 102 m × 5 × 102 m
= 40 × 104 m2
Area of the circle is = 4.0 × 105 m2
3. Two spheres of same size are made from copper and iron respectively. Find the ratio between their masses. Density of copper 8,900 kg/m3 and iron 7,800 kg/m3.
Volume of Copper Sphere = Volume of iron Sphere
Vcu = VFe ……………. (1)
mass = volume × density
M = V × d
mass ratio is
Mcu = MFe
Vcu × 8,900 hg/m3 : VFe × 7,800 hg/m3
Vcu × 89 : VFe × 78
89 : 78
Ratio of mass of spheres of Copper and Iron is = 89 : 78
4. A liquid having a mass of 250 g fills a space of 1000 cc. Find the density of the liquid.
Mass of the liquid = 250 g
Volume of the liquid = 1000cc
= 250 g / 1000cc = 0.25 g/cc
Density of the liquid = 0.25g cc-1
5. A sphere of radius 1cm is made from silver. If the mass of the sphere is 33g, find the density of silver. (Take π = 3.14).
Radius ofthe silver sphere = 1cm
Its mass = 33 g
Volume of the sphere = 4/3 πr3
= 4/3 × 3.14 × (1 cm)3
= 4/3 × 3.14 × 13 cm3
Density of sphere (d) = Mass / Volume
= (33 / 3.14) × 3/4 × g.cm-3
Density of sphere = 7.88 g/cm3
XIII. Cross word puzzle:
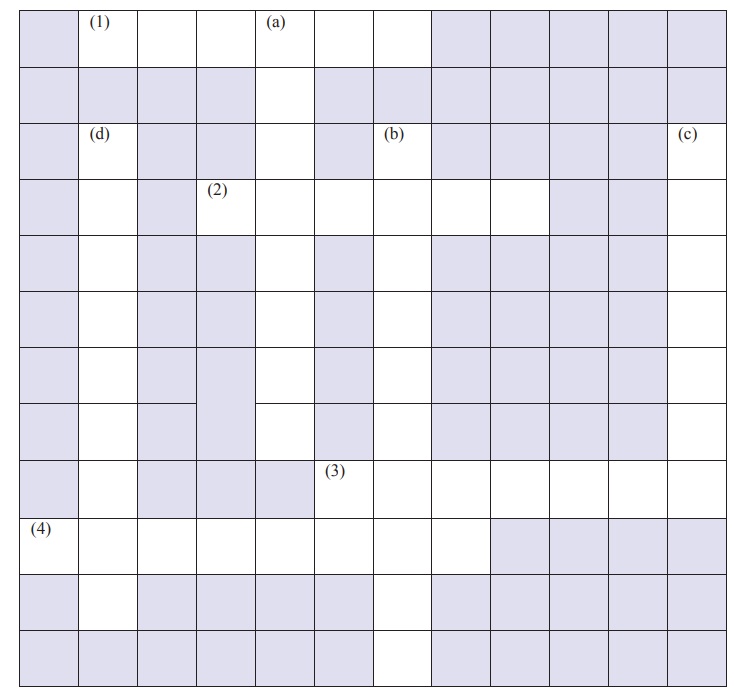
CLUES – ACROSS
1. SI unit of temperature
2. A derived quantity
3. Mass per unit volume
4. Maximum volume o liquid a container can hold
CLUES – DOWN
a. A derived quantity
b. SI unit of volume
c. A liquid denser than iron
d. A unit of length used to measure very long distances
Ans: [1. Kelvin; 2. Volume; 3. Density; 4. Capacity]
[a. Velocity; b. Cubic metre; c. Mercury; d. Lightyear]

Answer:
[1. Kelvin; 2. Volume; 3. Density; 4. Capacity]
[a. Velocity; b. Cubic metre; c. Mercury; d. Lightyear]














